Οι γωνιάσεις, κύριο χαρακτηριστικό του συμφυούς παραστήματος. Τα παραστήματα είναι τα τρία τέταρτα του στυλ
Δεν σας κρύβω ότι στην προσέγγιση μου για την παρουσίαση των γωνιάσεων του «Μπρετόν» έχω εμπνευστεί πάρα πολύ από τη σύλληψη των σχεδίων του καθηγητή SOLARO τα οποία απεικονίζονται στο βιβλίο του «Σκιαγράφημα περιγραφής του Πόιντερ του» (εκδόσεις E.N.C.I. – Μιλάνο). Την τελειότητα αυτής της μελέτης, απ’ ότι γνωρίζω, δεν την έχει ποτέ φτάσει κανένας άλλος για τους κυνηγετικούς σκύλους. Ο Πρόεδρος MARTINAU εμπνεύστηκε από αυτό και το χρησιμοποίησε ως βάση των δύο διαδοχικών πλακετών του Γαλλικού Ομίλου Πόιντερ σχετικών με τα σχόλια του προτύπου της ράτσας. Αυτές οι μελέτες παραμένουν παραδειγματικές και είναι κατά τη γνώμη μου, πραγματικά αξιόπιστες. Αναπόφευκτα, έχω αναλύσει και άλλες τις οποίες δεν συγκράτησα : Α! Αυτές οι περίφημες μελέτες...! Αγνοώντας τους τρόπους που λειτουργούν αυτοί οι συγγραφείς, έχω φανταστεί μια γραφική αναπαράσταση της επιθυμητής δομής του σκελετού του Μπρετόν από ενδεικτικές διαστάσεις που έχουν καταμετρηθεί σε πολλούς σκύλους οι οποίες εκφράζουν το πραγματικά συμφυές παράστημα.
Όμως ποιες διαστάσεις ; και με ποια ακρίβεια ; Έχω εξακριβώσει ότι μια απόκλιση μεγαλύτερη ή μικρότερη από ένα εκατοστό δεν θα μπορούσε να αλλοιώσει πραγματικά τις γωνιακές τιμές οι οποίες επιτρέπουν τις ποσοτικές αξιολογήσεις με μια ακρίβεια πέντε βαθμών. Παραμένοντας αντικειμενικοί παραμένουμε αξιόπιστοι. Όπως πάντοτε πρέπει να τηρούμε τόσο τις ανατομικές πραγματικότητες όσο και τις μηχανικές που σχετίζονται με την κίνηση.
Ακόμη και εάν επαναλαμβάνω τον εαυτό μου, οι γωνιάσεις προσδιορίζονται αφενός από τα μήκη των ακτινών των οστών (μηριαίο, περόνη, βραχιόνιο, κ.λ.π.) αλλά ειδικότερα από τα γωνιακά ανοίγματα μεταξύ δύο διαδοχικών γωνιών των οποίων ο συγκεκριμένος άξονας ταλάντωσης κατά την κίνηση είναι οι πραγματικές κορυφές των τιμών που πρέπει να προσδιοριστούν. Έχω διαπιστώσει μερικούς προσδιορισμούς επί του προκειμένου περισσότερο θεωρητικούς παρά πραγματικά μηχανικούς. Είναι γι’ αυτό που έχω συγκρατήσει αυτούς που μου φαίνονται πιο ρεαλιστικοί μηχανικά, δηλαδή αυτούς του δόκτορα HEROUT από τους οποίους ο LUQUET έχει ιδιαίτερα εμπνευστεί.
Λοιπόν πώς ένα χειριστής «λάμδα» αποφασίζει, διαθέτοντας ένα αναστημόμετρο (για τα ύψη από το έδαφος) ενός κοινού μέτρου ονομαζόμενο της μοδίστρας αλλά προικισμένος (εννοώ τον χειριστή) με λίγη λογική και μερικές μαθηματικές γνώσεις σχεδόν στοιχειώδεις ;
Στο σχολείο, όταν πέρασα το «Πιστοποιητικό», ο δάσκαλος με έμαθε (όπως και τους άλλους εξάλλου) να κατασκευάζω ένα οποιοδήποτε τρίγωνο γνωρίζοντας απλά τα μήκη των τριών πλευρών χρησιμοποιώντας μια ρίγα για τη βάση και ένα μοιρογνωμόνιο για εντοπισμό δια της τομής της τρίτης κορυφής του τριγώνου. Θυμάμαι ότι θίξαμε επίσης το θεώρημα του Πυθαγόρα. Πολύ πιο αργότερα επαγγελματικά, έμαθα ότι γνωρίζοντας τα μήκη των πλευρών αυτού του ίδιου τριγώνου, μπορούσαμε να υπολογίσουμε τις τιμές της κάθε μιας γωνίας. Απλή φόρμουλα του «Trigo» δηλαδή : Εφαπτομένη μιας γωνίας Α/2 = ρίζα του .. κ.λ.π., κ.λ.π.
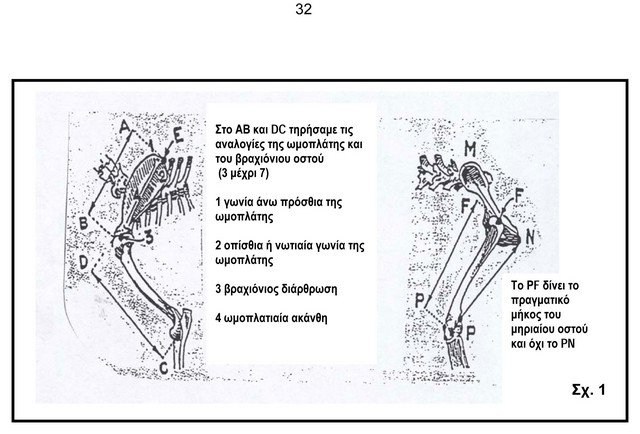
Τα πιο πάνω σχέδια του HEROUT, παρουσιάζουν τα κύρια σημεία αναφοράς των οστών (είτε μπορούμε να τα ψηλαφίσουμε είτε όχι) τα οποία επιτρέπουν την πλάγια ανάλυση σε διάφορα τρίγωνα του σκελετού του «Μπρετόν» (ειδικότερα του μπροστινού ποδιού όπως και του πίσω ποδιού), τρίγωνα των οποίων οι κορυφές είναι ακριβώς οι άξονες ταλάντωσης των κινήσεων προώθησης που καθορίζουν τα παραστήματα.
Όμως ποιες είναι ακριβώς οι σωματικές διαστάσεις και τα κάθετα ύψη που πρέπει να μετρηθούν ;
Λεπτομέρειες των διαστάσεων και των διορθώσεων των αρθρώσεων
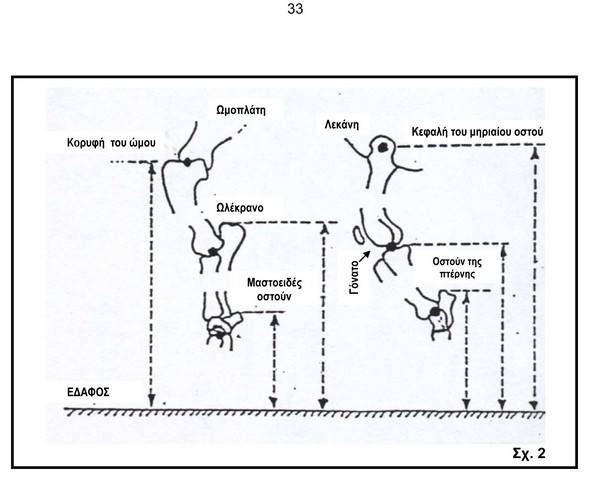
Διορθώσεις που πρέπει να γίνουν για τον εντοπισμό με ακρίβεια των αξόνων των αρθρώσεων οι οποίες εντοπίστηκαν με ακτινογραφία. Ακριβή ύψη της κορυφής του ώμου, της κεφαλής του μηριαίου οστού και της άρθρωσης του γονάτου. Αφού το σώμα του Μπρετόν περιγράφεται μέσα σε ένα τετράγωνο, το πρόσθιο άνω μέρος της βραχιόνιου διαρθρώσεως, η κορυφή του ακρωμίου καθώς επίσης η άκρη του γλουτού βρίσκονται αναγκαστικά επί των πλευρών του τετραγώνου αντίστοιχα με τα ύψη που καταγράφηκαν.
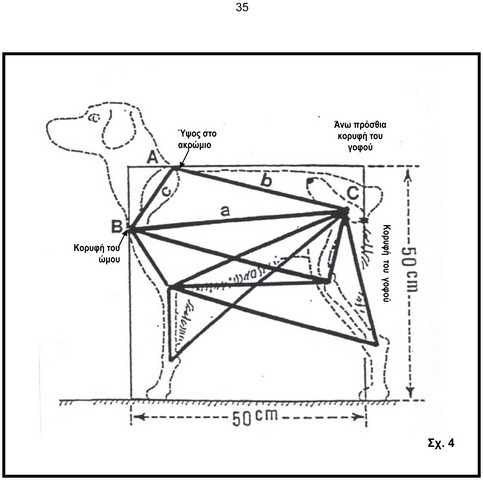
Ένα εύκολο παράδειγμα για την τοποθέτηση της ωμοπλάτης. Αφού το σώμα του Μπρετόν περιγράφεται μέσα σε ένα τετράγωνο, σχηματίστε ένα τετράγωνο σε οποιαδήποτε κλίμακα στο οποίο μεταφέρουμε, με την ίδια κλίμακα τις αποστάσεις ή ύψη που καταμετρήθηκαν.
Γνωρίζοντας τις αποστάσεις a-b και c και τις αποστάσεις A-B και C, το Α θα τοποθετηθεί στην άνω πλευρά του τετραγώνου. Το Β τοποθετείται στην αριστερή πλευρά στο ύψος που καταμετρήθηκε. Όσον αφορά το C θα τοποθετηθεί πάνω σε μια παράλληλη γραμμή με το έδαφος στο ύψος που καταμετρήθηκε. Από το Β, η εφαρμογή των αποστάσεων a-b και c προσδιορίζουν τη διατομή των τοποθετήσεων των κορυφών A και C.
Μετά από την «τοποθέτηση» καθαρά γραφική αλλά βασισμένη επί των αριθμών, ας προσεγγίσουμε τις αριθμητικές αξιολογήσεις των σχετικών μήκων και γωνιών μεταξύ δύο κορυφών ή αξόνων ταλαντώσεων.
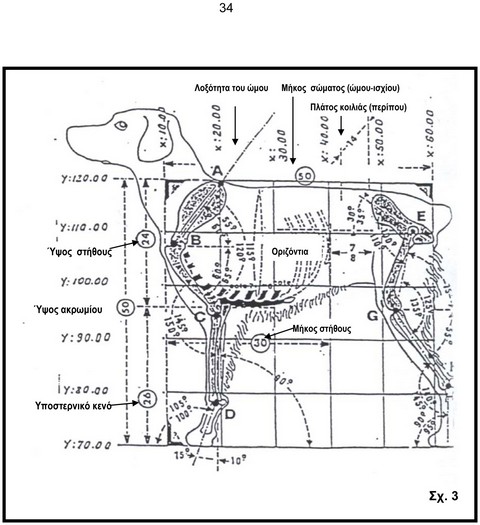
Πάνω σε αυτό το τετράγωνο (συμβατικό για τον «Μπρετόν» Yψος=Μήκος > από 50 εκατοστά της πλευράς) έκανα μια ορθογώνια χάραξη 10 εκατοστών, αναπαραστάνοντας οριζόντια τον άξονα των Χ και κάθετα τον άξονα των Y ώστε να βρούμε τις γραφικές συντεταγμένες, αρκετά ακριβείς, των κορυφών, ειδικότερα για την εφαρμογή των ακτινογραφικών διορθώσεων αφού είναι στην ίδια κλίμακα.
Γνωρίζοντας αυτά τα δεδομένα και ως παράδειγμα τις κορυφές Α και Β, ο υπολογισμός των αντίστοιχων διαφορών σε Χ και Y αντιστοιχεί με τις δύο πλευρές ενός ορθογώνιου τριγώνου. Η απλή εφαρμογή του θεωρήματος του Πυθαγόρα (τετράγωνο της υποτείνουσας.... κ.λ.π.) σας δίνει την απόσταση μεταξύ Α και Β δηλαδή το μήκος της ακτίνας ή του τμήματος του συγκεκριμένου οστού.
Τώρα ας προσεγγίσουμε τις αξιολογήσεις των γωνιών. Πάντοτε ξεκινώντας από τις κορυφές Α και Β των οποίων οι διαφορές σε Χ και Y είναι γνωστές (βλέπε πιο πάνω), διαιρώντας αυτές τις διαφορές την μια με την άλλη ή αντίστροφα, λαμβάνουμε τις τριγωνομετρικές τιμές (εφαπτομένη ή συνεφαπτομένη) της γωνίας που σχηματίζει η ακτίνα ΑΒ με την οριζόντια ή την κάθετη γραμμή. Ενας απλός υπολογισμός εφοδιασμένος με αυτές τις τιμές, ονομαζόμενες φυσικές, σας δίνει την αντίστοιχη γωνία. Με μετάθεση και πρόσθεση, λαμβάνουμε τις αναζητούμενες αξίες CQFD.
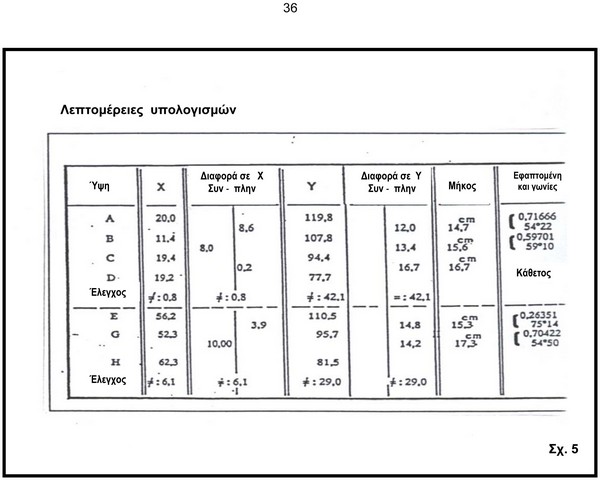
Λεπτομέρεια των υπολογισμών
Πρακτική απόδειξη όμως αριθμητικά αδιαμφισβήτητη. Σίγουρα είναι επαγγελματικά κατάλοιπα, αλλά πάντοτε είχα περισσότερη εμπιστοσύνη στους αριθμούς παρά στη φιλολογία. Θα τελειώσω παραθέτοντας τον φυσιολόγο Claude BERNARD και το βιβλίο του «Μελέτη της εμπειρικής ιατρικής».
«Η εμπειρική μέθοδος προχωρεί αργά και υπό αυτή την έννοια θα αρέσει πάντοτε λιγότερο στο πνεύμα».
Jean LOUVET
Επίμονες παρατηρήσεις «μερικών» αβέβαιων με προκάλεσαν να δικαιολογηθώ. Εξ’ ου και αυτό το μαθηματικό συμπλήρωμα. Πράγμα που έγινε !
Τώρα γι’ αυτούς του δύσπιστους και τους ομοϊδεάτες τους, θα αναφέρω τον καθηγητή Queinnec : «Στη φύση και ακόμη καλύτερα κατά τη διάρκεια μιας ειδικής επιλογής, όσο επιζητούμε το ίδιο όργανο διαπιστώνουμε την ανάπτυξη του κατά τρόπο ειδικό σε ποιότητα και χαρακτήρα που μεταδίδονται κληρονομικά».
 |
 |
 |
 |
 |
 |




